比的意义

两个数相除又叫作两个数的比。比的前项除以后项所得的商叫做比值。比的前项和后项只有公因数1的比叫作最简整数比。

例如：7:8中，7和8是互质数，所以7:8是一个最简整数比。7÷8=，是7:8的比值。

求比值

比的前项除以后项所得的商叫求比值。求比值的方法为用比的前项除以后项（前项÷后项）。比值是一个数（整数、小数或分数都可以）。

化简比

前项和后项互质。

化简比的方法为：比的前项和后项同时乘或除以相同的数（0除外）；求比值，再将此值写成最简比。

一个比（有前项和后项），也可以写成分数形式，但不能写成带分数、小数或整数。

例如：20:30，比值2:3。

比和分数、除法的关系表

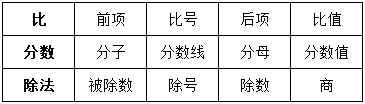
比的基本性质

比的前项和后项都乘或除以相同的数（0除外），比值不变。

当一个比是两个同类量相比，前项和后项单位不同时，要先化成相同的单位，然后才能求比值或化简比。

例如：1米:1厘米=100厘米:1厘米=100:1

比例

比例的意义与基本性质

表示两个比相等的式子叫作比例。

如：100:10=20:2，其中100与2叫是这个比例的外项，10和20是这个比例的内项。

在比例里，两个外项的积等于两个内项的积。即：a:b=c:d，则：ad=bc。

如何判断两个比能否成比例

1、把两个比的比值求出来，看比值是否相等，如果相等，就能组成比例。

例如：100:10=10:1，20:2=10:1。所以100:10=20:2可以组成比例。

2、假设两个比能组成比例，计算两个内项和积是否等于两个外项的积。

假设：100:10=20:2，100×2=200，10×20=200，两个内项积等于两个外项积，可以组成比例。

解比例

在一个比例里，已知其中的三个项，求另一个项，可以根据比例的基本性质，把比例写成两个积相等的等式，再求出等式中的未知项就是解比例。

例如：3:5=a:30，求a。

5×a=3×30

a=90÷5=18

按比例分配

把一个数量按照一定的比分配，这种分配方法通常称为按比例分配。

比例尺

在绘制地图或其他平面图时，常常需要把实际距离缩小或扩大若干倍画在图纸上。图上距离和实际距离的比叫作这幅图的比例尺。

比例尺的表示方法有：数字比例尺与线段比例尺。

数字比例尺，1：5000000表示图上1厘米表示实际5000000厘米（50千米）；

线段比例尺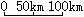，表示1厘米表示实际50千米。

比例尺的前项为1，如1：8，表示把实际距离缩小到原来的1/8画在图上。后项为1，如8：1，表示把实际距离扩大8倍画在图上。

图上距离：实际距离=比例尺

实际距离=图上距离÷比例尺

图上距离=实际距离×比例尺

比例尺是一个比，在计算中，用比例尺的比值进行计算。如果是最后求比例尺，结果要写成比的形式，一般写成前项（或后项）为1的比。

图形的放大与缩小

图形的放大与缩小是按照一定的比例把物体或图形放大或缩小，然后画在图纸上。图形放大时，放大的比例是一个后项为1的比，如放大3倍，就是按3：1放大；图形缩小时，缩小的比例是一个前项为1的比，如缩小到原来的1/3，就是按1：3缩小。

正比例和反比例

正比例

两种相关联的量，已知一种量变化，另一种时也随之变化，如果两种量中对应的两个数的比值（也就是商）一定，这两种量就叫作成正比例的量。

正比例的关系式：用字母x表示一个变量，用字母y表示另一个量，用字母k表示比值（也就是商）一定。=k(一定)。

反比例

两种相关阳的量，已知一种量变化，另一种量也随之变化，如果两种量中相对应的两个数的积一定，这两种量就叫作成反比例的量。

反比例的关系式：用字母x表示一个变量，用字母y表示另一个量，用字母k表示积一定。xy=k（一定）。

比值一定，成正比例；

积一定，成反比例；

比值和商都不一定，不成比例。