在整数除法中，如果商是整数而没有余数，我们就说被除数是除数的倍数，除数是被除数的因数（约数）。

如：12÷2=6，我们就说12是2的倍数，2是12的因数。

完全数（完美数）：6的因数有1，2，3，6这几个因数的关系是1+2+3=6。像6这样的数，叫做完全数（也叫完美数）。

奇数与偶数

整数中，是2的倍数的数叫做偶数（0也是偶数），不是2的倍数的数叫做奇数。

奇数+偶数=奇数；奇数+奇数=偶数；偶数+偶数=偶数。

3的倍数特征：一个数各位上的数的和是3的倍数，这个数就是3的倍数。如：12，1+2=3；33，3+3=6，87，8+7=15。

质数与合数

一个数，如果只有1和它本身两个因数，那么这样的数叫做质数（或素数）。如2，3，5，7等。

一个数，如果除了1和它本身还有别的因数，那么这样的数叫做合数。如4，6，15，49等。

每个合数都可以由几个质数相乘得到。例如：4=2×2，15=3×5等。

其中每个质数都是这个合数的因数，叫做这个合数的质因数。

最大公因数

1，2，4是8和12公有的因数，叫做它们的公因数。其中，4是最大的公因数，叫做它们的最大公因数。

利用分解质因数的方法，可以比较简便地求出两个数的最大公因数。例如：

24=2×2×2×3

36=2×2×3×3

22和36的最大公因数：2×2×3=12

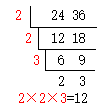
约分

把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。

分子和分母只有公因数1，这样的分数叫做最简分数。约分时，通常要约成最简分数。

如：。

最小公倍数

12，24，36，都是4和6公有的倍数，叫做它们的公倍数。

其中，12是最小的公倍数，叫做它们的最小公倍数。没有最大的公倍数。

也可以利用分解质因数的方法，比较简便地求出两个数的最小公倍数。例如：

60=2×2×3×5

42=2×3×7

60和42的最小公倍数：2×3×2×5×7=420

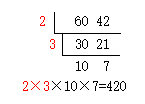
分数的大小比较-通分

分母相同时，分子大的分数就越大。分子相同时，分母大的分数反而越小。

如何比较分子与分母都不相同的分数呢？

把异分母分数分别化成和原来分数相等的同分母分数，叫做通分（即用两个分母的公倍数作公分母）。如：

和

分数的大小比较-转为小数后比较

把分数的分母分解质因数，就能知道一个分数能否化成有限小数。如果分母中除了2和5以外，不含有其它质因数，这个分数就能化为有限小数。如果分母中含有2和5以外的质因数，这个分数就不能化成有限小数。

如：的分母20=2×2×5，可以化成小限小数。0.05

的分母30=2×3×5，它就不能化成有限小数。0.233333333...