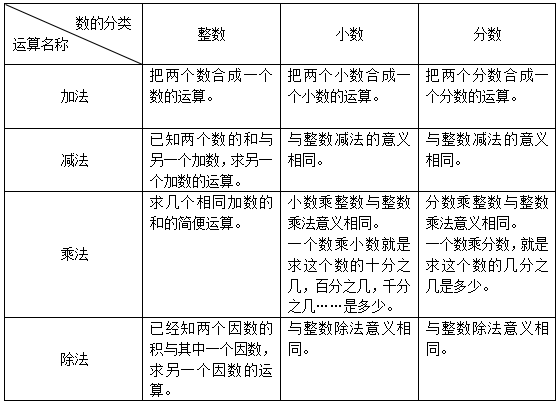
四则运算的意义
四则运算的法则
整数加减法
1、相同数位对齐;
2、从低位算起;
3、加法中满几十就向前一位进几;减法中不够减时,就从前一位借,借几就当几十。
小数加减法
1、相同数位对齐(小数点对齐);
2、从低位算起;
3、按整数加减法法则进行计算;
4、结果中的小数点和相加减的数里的小数点对齐。
分数加减法
1、同分母分数相加减,分母不变,分子相加减;
2、异分母分数相加减,先通分,然后计算;
3、结果能约分的要约分。
整数乘法
1、从个位乘起,依次用第二个因数每位上的数去乘第一个因数;
2、用第二个因数哪一位上的数去乘,得数的末位就和第二个因数的那一位对齐;
3、再把几次乘得的数加起来。
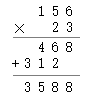
小数乘法
1、按整数乘法的法则先求出积;
2、看因数中一共有几位小数。就从积的右边起数出几位点上小数点。
如:15.6×2.3=35.88
分数乘法
1、分数乘分数,用分子相乘的积作分子,分母相乘的积作分母;
2、有整数的把整数看作分母是1的假分数;
3、有带分数的通常先把带分数化成假分数。
如:×3=
×
,
×
=
×
整数除法
除数是整数的除法:从被除数的高位起,除数是几位数,就先看被除数的前几位,如果不够除,就要多看一位。除到哪一个就把商写在那一位上面。商的小数点和被除的小数点对齐。
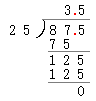
小数除法
被除是小数的除法:先移动除数的小数点,使它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补“0”),然后按照除数是整数的除法进行计算。
分数除法
甲数除以乙数(0除外),等于甲数乘以乙数的倒数。
如:÷
=
×
四则运算各部分之间的关系
加数+加数=和
一个加数=和-另一个加数
被减数-减数=差
被减数=差+减数
减数=被减数-差
因数×因数=积
一个因数=积÷另一个因数
被除数÷除数=商
在有余数除法中,各部分有下面的关系:
被除数=除数×商+余数
除数=(被除数-余数)÷商
四则运算的顺序
先乘除、后加减,有括号的要先算括号里的,再算括号外面的,如果有小括号、中括号,先算小括号里面的再算中括号里面的。
运算性质
减法的运算性质:
a-(b+c)=a-b-c;a-(b-c)=a-b+c
除法的运算性质:
a÷(b×c)=a÷b÷c
a÷(b÷c)=a÷b×c
(a+b)÷c=a÷c+b÷c
(a-b)÷c=a÷c-b÷c
和、差、积、商的变化规律
和
加法中,加数增加(或减少)一个数,和也随着增加(或减少)同一个数;
当一个加数增加一个数,另一个加数减少同一个数时,和不变。
a+b=c
(a+m)+(b-n)=c+m-n
(a+m)+(b-m)=c
积
乘法中,因数乘上(或除以)一个数(不为0),积也随着乘上(或除以)这个数;
当一个因数乘上(或除以)一个数(不为0),另一个因数除以(或乘上)这个数时,它们的积不变。
a•b=c
(a•m)•(b÷n)=c•m÷n
(a•m)•(b÷m)=c
差
减法中,被减数加上(或减去)一个数,差也随着增加(或减少)同一个数;被减数加上(或减去)一个数,差反而减少(或增加)一个数;
当被减数和减数都加上(或减去)同一个数时,它们的差不变。
a-b=c
(a±m)-b=c±m
a-(b±m)=c±m
(a±m)-(b±m)=c
商
除法中,被除数乘上(或除以)一个数(不为0),除数不变,商也随着乘上(或除以)这个数;被除数不变,除数乘上(或除以)一个数(不为0),商则除以(或乘上)这个数;
被除数和除数同时乘上(或除以)一个数(不为0),其商不变。
a÷b=c
(a•m)÷b=c•m
(a÷m)÷b=c÷m
a÷(b•m)=c÷m
a÷(b÷m)=c•m
(a•m)÷(b•m)=c
(a÷m)÷(b÷m)=c
有关“0”和“1”的运算
a+0=a;a-0=a;a-a=0;
a•0=0;0÷a=0(a≠0);
a•1=a;a÷1=a;a÷a=1(a≠0);1÷a=(a≠0)

